Welcome to DU!
The truly grassroots left-of-center political community where regular people, not algorithms, drive the discussions and set the standards.
Join the community:
Create a free account
Support DU (and get rid of ads!):
Become a Star Member
Latest Breaking News
Editorials & Other Articles
General Discussion
The DU Lounge
All Forums
Issue Forums
Culture Forums
Alliance Forums
Region Forums
Support Forums
Help & Search
I merely integrated twice as described below:
Let's do something very, very, very crude, just as an illustration with the understanding that it is unsophisticated but may be illustrative:
As of this writing, I have been a member of DU for 19 years and 240 days, which works out in decimal years to 19.658 years. This means the second derivative, the rate of change of the rate of change is 0.04 ppm/yr^2 for my tenure here. (A disturbing fact is that the second derivative for seven years of similar data running from April of 1993 to April of 2000 showed a second derivative of 0.03 ppm/yr^2; the third derivative is also positive, but I'll ignore that for now.) If these trends continue, this suggests that “by 2050,” 28 years from now, using the language that bourgeois assholes in organizations like Greenpeace use to suggest the outbreak of a “renewable energy” nirvana, the rate of change, the first derivative, will be on the order of 3.6 ppm/year. Using very simple calculus, integrating the observed second derivative twice, using the boundary conditions – the current data - to determine the integration constants, one obtains a quadratic equation (0.04)t^2+(2.45)t+ 419.71 = c where t is the number of years after 2022 and c is the concentration at the year in question.
If one looks at the data collected at the Mauna Loa displayed graphically, one can see that the curve is not exactly linear, but has a quadratic aspect somewhat hidden by the small coefficient (0.04) of the squared term:
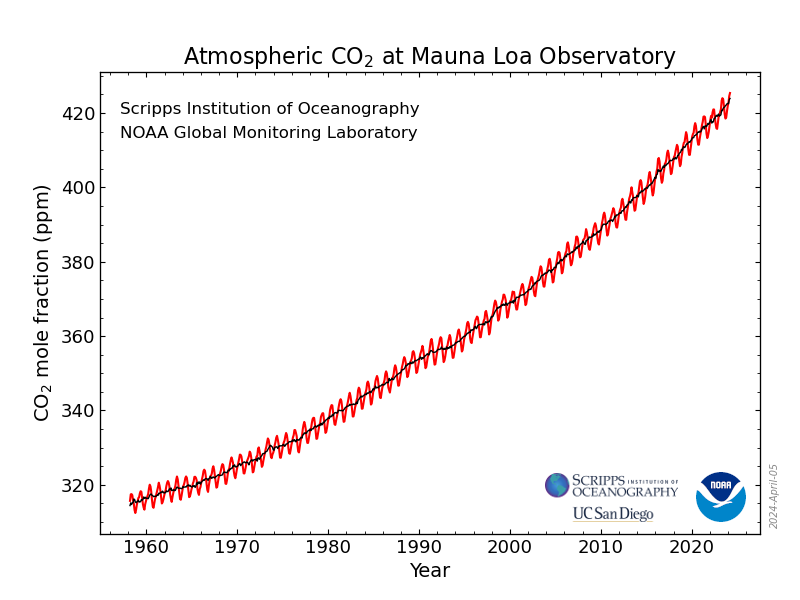
As of this writing, I have been a member of DU for 19 years and 240 days, which works out in decimal years to 19.658 years. This means the second derivative, the rate of change of the rate of change is 0.04 ppm/yr^2 for my tenure here. (A disturbing fact is that the second derivative for seven years of similar data running from April of 1993 to April of 2000 showed a second derivative of 0.03 ppm/yr^2; the third derivative is also positive, but I'll ignore that for now.) If these trends continue, this suggests that “by 2050,” 28 years from now, using the language that bourgeois assholes in organizations like Greenpeace use to suggest the outbreak of a “renewable energy” nirvana, the rate of change, the first derivative, will be on the order of 3.6 ppm/year. Using very simple calculus, integrating the observed second derivative twice, using the boundary conditions – the current data - to determine the integration constants, one obtains a quadratic equation (0.04)t^2+(2.45)t+ 419.71 = c where t is the number of years after 2022 and c is the concentration at the year in question.
If one looks at the data collected at the Mauna Loa displayed graphically, one can see that the curve is not exactly linear, but has a quadratic aspect somewhat hidden by the small coefficient (0.04) of the squared term:
I originally did this in this post:
A Commentary on Failure, Delusion and Faith: Danish Data on Big Wind Turbines and Their Lifetimes.
The thread was taken up by real, real Dunning-Kruger type of antinuke, one so ignorant as to be sure to reinforce his or her or their ignorance, including a precious announcement that nuclear energy is dangerous because of the generation of 139Ba which the poster claimed decayed into a "toxic element." The half-life of 139Ba is about 83 minutes, and it decays into stable lanthanum, which is certainly not an element known to be especially toxic, but is often included in electronic devices.
One hears these sorts of things and one doesn't really want to believe it.
It is, of course, somewhat amusing to hear just how uneducated antinukes can be, but that one has to be a classic, almost as dumb as a poster over at the benighted DailyKos website who went by a name I won't share, who once listed a bunch of half-lives for radionuclides, maybe 10 or 15, with not one - not even one - being even remotely correct. One wonders where these people get this stuff, and how they manage proudly to advertise, indeed parade, their ignorance.
(I'm sort of pleased that I was banned at DailyKos for telling the truth. Some of the people there, that one included, were unbearably, depressingly poorly educated, but nonetheless took themselves all too seriously. Hence the burning planet. I surely don't miss that place.)
I suppose one could integrate to an exponential by assuming that the rate was proportional to time, but I don't think over the range of data it would give an especially different result. I wanted to limit the analysis to high school calculus.
Edit history
Please sign in to view edit histories.
Recommendations
0 members have recommended this reply (displayed in chronological order):
2 replies
= new reply since forum marked as read
= new reply since forum marked as read